2024年重庆市物理高考第15题原题呈现
15.（18分）如图所示，$M$、$N$两个钉子固定于相距$a$的两点，$M$的正下方有不可伸长的轻质细绳，一端固定在$M$上，另一端连接位于$M$正下方放置于水平地面质量为$m$的小木块$B$，绳长与$M$到地面的距离均为10$a$，质量为2$m$的小木块$A$，沿水平方向于$B$发生弹性碰撞，碰撞时间极短，$A$与地面间摩擦因数为$\mu$，重力加速为$g$，忽略空气阻力和钉子直径，不计绳被钉子阻挡和绳断裂时的机械能损失。
（1）若碰后，B在竖直面内做圆周运动，且能经过圆周运动最高点，求B碰后瞬间速度的最小值；
（2）若改变$A$碰前瞬间的速度，碰后$A$运动到$P$点停止，$B$在竖直面圆周运动旋转2圈，经过$M$正下方时细绳子断开，$B$也来到$P$点，求$B$碰后瞬间的速度大小；
（3）若拉力达到12$mg$细绳会断，上下移动$N$的位置，保持$N$在$M$正上方，B碰后瞬间的速度与（2）间中的相同，使$B$旋转$n$圈。经过$M$正下的时细绳断开，求$MN$之间距离的范围，及在$n$的所有取值中，$B$落在地面时水平位移的最小值和最大值。
解题思路
第一问
(1)若碰后，B在竖直面内做圆周运动，且能经过圆周运动最高点，求B碰后瞬间速度的最小值；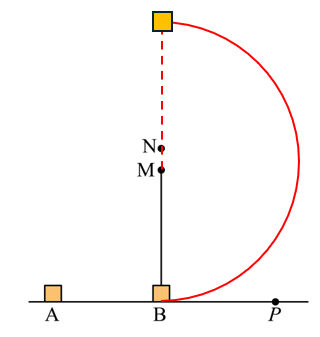
该题分析最高点即可，但学生可能分不清楚最高点分析是是以谁为圆心，应以引导。
解：最高点以M为圆心，由牛二：
$$ mg=\frac{mv^2}{10 a} $$
又动能定理：
$$ \frac{1}{2} mv_1^2 -\frac{1}{2}mv_2^2 =mg·20a $$
解得$v_1=\sqrt{2ga}$
第二问
(2)若改变A碰前瞬间的速度，碰后A运动到P点停止，B在竖直面圆周运动旋转2圈，经过M正下方时细绳断开，B也来到P点，求B碰后瞬间的速度大小；
该题突破点在于两个物体运动的关联
关联1：双守恒可知碰后速度比为$v$、$4v$
关联2：A减速运动和B平抛水平位移相同
解：
由弹性碰撞：
$$ 2mv_A=2mv'_A+mv'_B $$
$$ \frac{1}{2}·2mv^2_A=\frac{1}{2}·2mv'^2_A+\frac{1}{2}mv'^2_B $$
解得
$$ v'_A=\frac{1}{3}v_A，v'_B=\frac{4}{3}v_A $$
碰后对A:
$$ \frac{1}{2}·2mv'^2_A=\mu· 2mgd $$
碰后对B：
$$ \frac{1}{2}mv'^2_B=mg·4a+\frac{1}{2}mv''^2_B \\ \frac{1}{2}gt^2=4a \\ v''_Bt=d $$
联立上式解得
$$ v'_B=4\sqrt{5ga}或\frac{4}{3}\sqrt{5ga}（小于v_1，舍去） $$
综上B碰后速度为$4\sqrt{5ga}$
整理算式的时候，可用v和4v分别来代换A、B的碰后速度，整理后得到关于v的四次方程:
$$ (16v^2 -8ga)·\frac{8a}{g}=24^2·\frac{v^4}{25g^2}$$
可令$x=v^2$，得
$$9x^2-50gax+25g^2a^2=0 $$
第三问
(3)若拉力达到12mg细绳会断，上下移动N的位置，保持N在M正上方，B碰后瞬间的速度与(2)问中的相同，使B旋转n圈．经过M正下方时细绳断开，求MN之间距离的范围，及在n的所有取值中，B落在地面时水平位移的最小值和最大值．
内容较多，首先引导学生分析条件和问题各是什么
条件：最大拉力12mg、B碰后速度$v''_B$、n圈、M正下方断开
问题1：MN取值范围
取值范围问题就是要“保证”条件成立，即保证绳子在M正下方断开，这也是本题难点：如何保证在第n圈时，绳子在M正下方断开?解决该问题的难点在于能分析出第n圈过程绳子的拉力如何变化。
可通过写向心力表达式分析出拉力
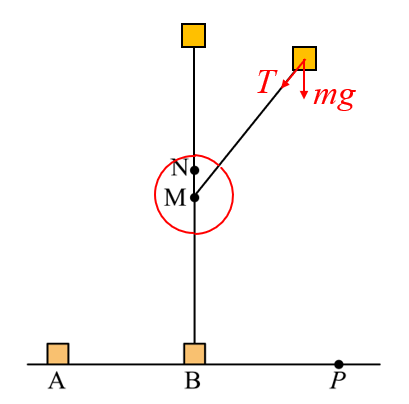
$$T=m\dfrac{v^2}{R}-mg\cos{\theta}$$
分析出位置越高速度越小拉力越小，碰到钉子瞬间速率不变半径变小，拉力突然变大通过下面的演示小程序，可以看到过程中拉力的变化。注意：N点钉子可以上下拖动调整位置。
分析出“保证”的条件：第n圈在M正下方以N为圆心绳不断，以M为圆心绳断。
解：第n圈在N点正下方时
$$ 𝑇_1−𝑚𝑔=\frac{𝑚𝑣_𝑁^2}{10𝑎−(2𝑛−1)ℎ} $$
由题意$T_1\leq 12mg$
在M点正下方时
$$ 𝑇_2−𝑚𝑔=\frac{𝑚𝑣_𝑀^2}{10𝑎−2𝑛ℎ} $$
由题意$T_2\geq 12mg$
解得
$$ \frac{5𝑎}{3𝑛}≤ℎ≤\frac{30𝑎}{18𝑛−11} $$
问题2：在n的所有取值中，B落在地面时水平位移的最小值和最大值．
该问题是对数学结果的物理分析，该题的设问对试题命制和日常教学有指导意义：要引导学生对某些数学结果进行反思与分析，反思结果符合实际情况，分析数学结果是否有规律、分析是否有取值上的最大和最小。
解决该问题首先要分析出B落地时的水平位移。该问题并不难。
对B由机械能守恒
$$ \frac{1}{2}𝑚𝑣_𝑛^2+𝑚𝑔𝑛ℎ=\frac{1}{2}𝑚𝑣'^2_B \\ \frac{1}{2}gt^2=nh \\ v_nt=s $$
联立上式解得
$$ 𝑠=4\sqrt{20𝑎·𝑛ℎ−(𝑛ℎ)^2} $$
分析根号下的二次函数，可知当$nh<10a$时，$s$随$h$单调递增
当$nh=\dfrac{5a}{3}$时，$s$最小为$\dfrac{20\sqrt{11a}}{3}$；
当$n=1$，$nh$最大为$\dfrac{30a}{7}$，$s$最大为$\dfrac{40}{7}\sqrt{33a}$
分析左边比较简单，右边需要尝试n在不同取值时的nh最大值
数学能力一直是重庆市物理压轴题考察比较多的关键能力。例如2021年的一元三次方程、2022年的轨迹交点二次函数根判别式、2023年等比数列，2024年的函数极值分析。